Introduction to Bayesian approach (lecture materials)

This illustrates the Bayesian updating rule graphically. First, have a look at the probability reminder (in French).

The model

Conditional and joint probabilities

We suppose that variable \(Z\) is tossed according to the following model, depending on a parameter \(\theta\).

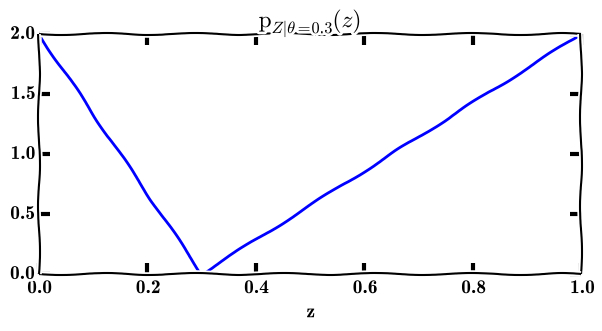
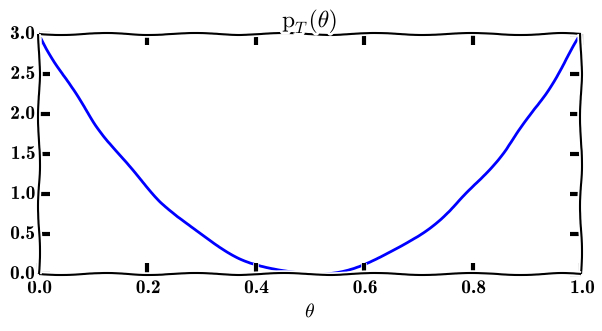
The Bayesian approach starts by considering that, before each toss of a sample \(z\), the parameter \(\theta\) is indeed tossed according to some variable \(T\). The law of that variable is arbitrary, let is consider a dummy parabolic one.

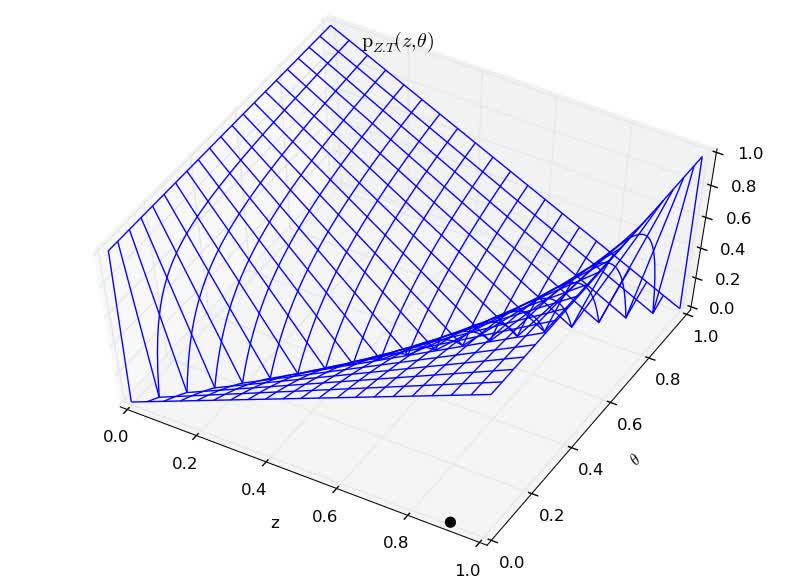
The joint variable \((Z, T)\) has therefore the following density of probability.

With several prior parameter distribution

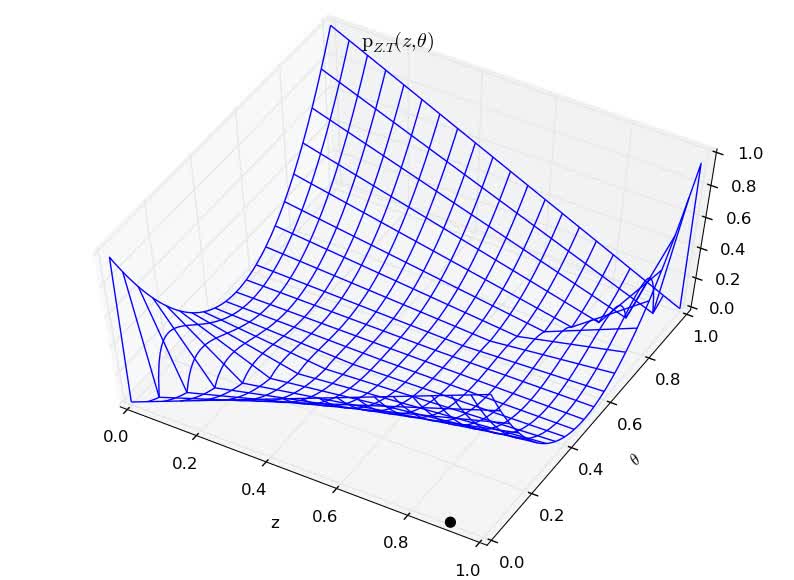
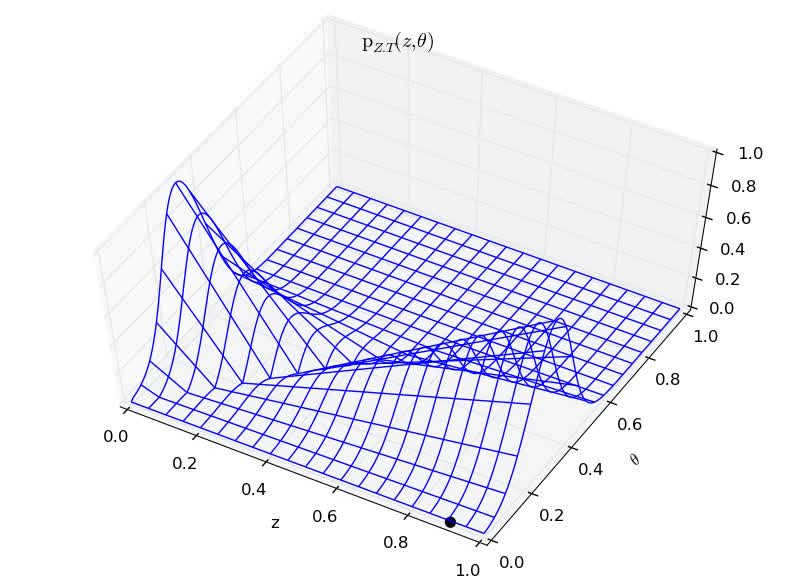
The Bayesian updating rule

The variable \(T\) is unknown, it is generally a Dirac, i.e. we always use the same value for \(\theta\). First, let us get a sample \(z\). The unknown oracle tosses \(\theta\) and then, according to the model \(P_{Z|\theta}(z)\), it tossed the actual sample \(z\). The oracle may not be ruled like this, but this is the way we have modelled it, explicitly.

As we know the joint variable \((Z,T)\), we can compute \(P_{T|z}(\theta)\).

We use this function as the new prior distribution of the variable \(T\)… which means that the density of the joint variable \((Z,T)\) can be recomputed.

The oracle tosses next sample \(z\), and we restart the update of \(T\).

Examples

In these examples, the oracle actually tosses \(z\) from the function \(P_{Z|\theta}(z)\) used in our model, but it always use \(\theta=0.7\). So \(z\) samples are provided according to \(P_{Z|T=0.7}(z)\). Let us see how the update of \(T\) from different priors finds that our oracle uses a constant \(\theta=0.7\).

Uniform prior

Parabolic prior

Gaussian prior

This shows that if \(\theta\) changes to another constant, the Bayesian update reconsiders its hypothesis about the \(T\) distribution.

Hervé Frezza-Buet,