Vector quantization with Graph Induced Topology

Graph Induced Topology (GIT)

Most of on-line vector-quantization algorithms rely on the weight update \(w_{t+1} = (1-\alpha)w_t + \alpha \xi_t\), modifying the prototype \(w\) when the input \(\xi_t\) is presented. This is illustrated below (left)

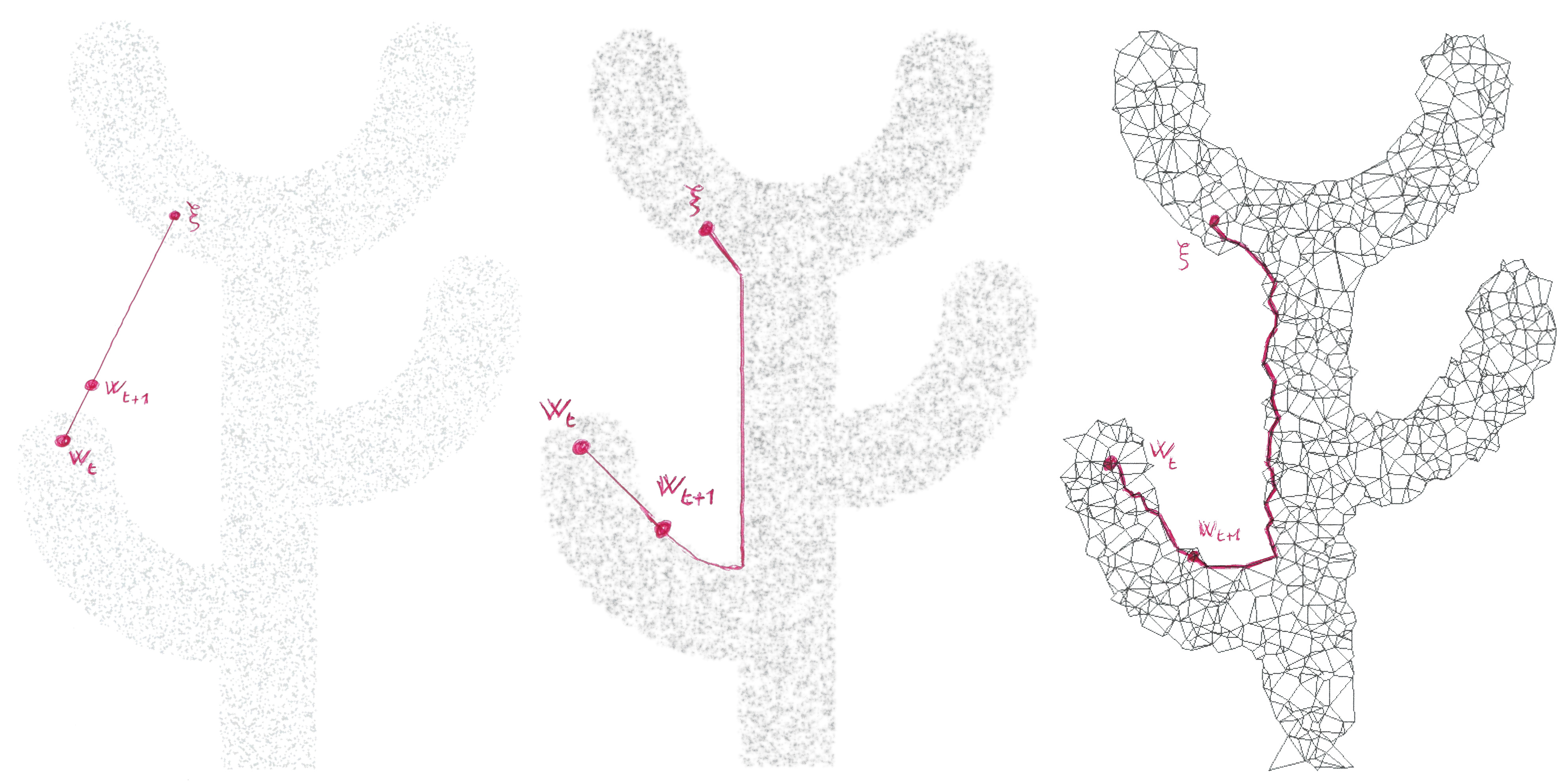
Left - Online VQ weight update in Euclidian 2D space. Middle - Idealized update if the topology of the cactus manifold were known. Right - Approximation based on a Compétitive Hebbian Learning graph

Thanks to Competitive Hebbian Learning (Martinez & Schulten, 1994), one can build a “masked Delaunay Triangulation” in order to cover the dataset with a graph. Then following shortest paths (from A* or Dijkstra) gives an update complient with a “Graph Induced Topology”

Re-visiting K-means with GIT

Here, we consider only the online version of k-means, since only the above update learning rule is avaiable to us (we cannot compute centroïds). First, let us see what the classical euclidian k-means does (\(k = 5\)).

From the same dataset, let us extract 10% of the points and use them as vertices of the CHL graph and build the graph from the whole dataset (1 pass only is required). Then we apply k-means with the GIT.

Some supplementary work is to be done for handling noise. Indeed, noise is quantified by vector quantization, leading to sparse prototype in noisy regions. The trick is to apply competitive Hebbian learning (CHL), and weight the edges according to the number of samples around them. Edges with low weight are considered as very long in the path computation.

Left - Noisy inputs. Middle - Weighted CHL. Right - Voronoï cells of the 3 central prototypes according to edges with modified lengths

The k-means handles the noise…

Non-Euclidian Travelling Salesman Problem

Ring-shaped 1D self-organizing maps enable to approximate a solution of the Eucidian Travelling Salesman problem (Euclidian TSP). This is illustrated below, wher the inputs are positions in the corridors of our first-floor.

The problem is said to be Euclidian since every point is supposed to be reachable from any other through a straight line. This is why you get a path crossing the walls.

The GIT-VQ approach copes with this limitation, once a graph is built beforehand thanks to CHL. The TSP is not Euclidian anymore but based on the inner topology of the manifold where the samples are taken from.

The approach is not specific to 2D, this illustrates the mechanism on a 3D artificial distribution.

References

Martinez, T. M., & Schulten, K. J. (1994). Topology Representing Networks. Neural Networks, 7(3), 507–522.

Hervé Frezza-Buet,